USNO A blue and red are often used as estimators of colour for stars. This despite no guarantees that the observations were contemporaneous. Though this is not a problem for constant stars, it can of course be a problem for variable stars.

USNO B1.0 is newly photometrically calibrated with respect to Tycho2 BT and VT photometry.

A May 2002 copy of loneos.phot, a critically compiled list of photometry by Brian Skiff, was used as a source of Johnson V and B-V photometry.

A 'list' of coordinates was generated using it and the USNO B1.0 was investigated via the CdS VizieR service, selecting objects within a search radius of 1 arcsec where data for both B1 and R1 was available (technically, where both B1 and R1 were non-null).

ASSUMPTIONS:

i) B1 and R1 are contemporaneous POSS I observations (same night 'back to back' exposures). This has been the case in every instance that I have double checked over the past few months via also requesting USNOFS images for various tasks. I have no concrete proof of this always absolutely being true, unfortunately.

ii) Despite differences in source astrometry, within 1 arcsec matches are assumed to be real matches and that any false cross identifications would only result in general scatter and not affect any trend within the data. Indeed, a large number of false matches would simply lead to a mess in the intended plot.

iii) Brian Skiff's loneos.phot file, by the nature of the specific pecularities of selection for the stars in it, is essentially random in terms of magnitude (within it's range), colour (although it is probably relatively light in terms of quite red stars), RA and Declination.

DATA RETURNED

The loneos file consisted of ~ 33,000 objects, 500+ entries were removed due to having no B-V value recorded.

Only single matches were kept, which resulted in the manual deletion of about a dozen "double hit" objects.

This resulted in 22,500+ matches with USNO B1.0 B1-R1 data.

An arbitrary decision was made to investigate only B1-R1 values, once calculated, between 0 and 4. This led to the removal of very nearly 600 negative B1-R1 values (including a dozen ridiculously large ones of up to -8) and about a dozen B1-R1 values between +4 to +10.

The final sample consisted of 21,911 objects.

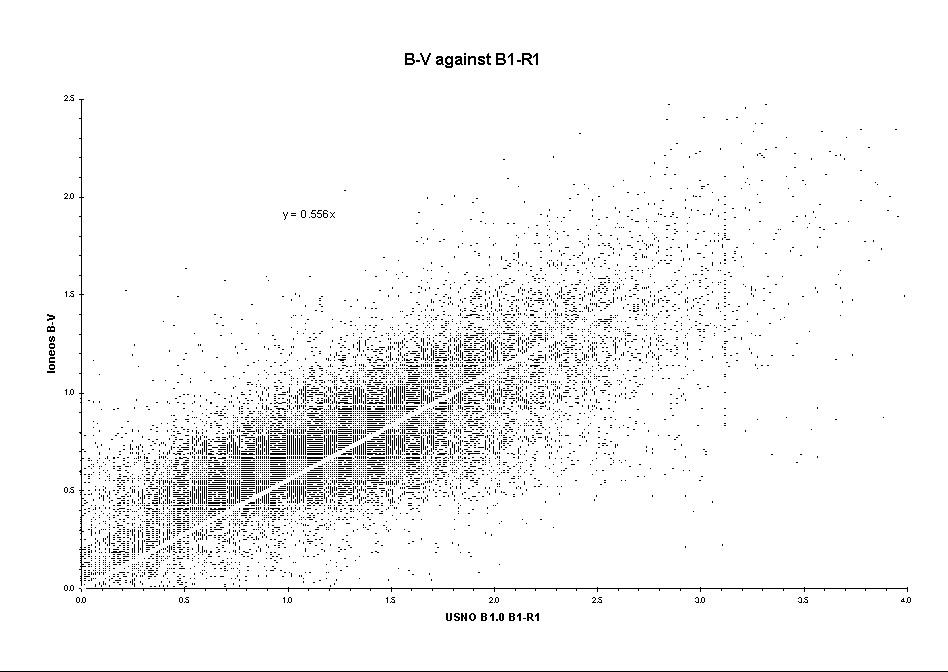
Plotting loneos B-V against B1-R1 led to attached graph BVBR.gif (interference effects due to the number of points have led to artificial patterning in the plot).

A linear fit gave B-V = 0.235 + 0.411(B1-R1) with correlation coefficient, R^2, of 0.59.

Adopting a zero intercept gave B-V = 0.556(B1-R1) with a correlation coefficient, R^2, of 0.50. (The white line in the graph).

Personally, I feel this difference in fit is sufficiently small to feel happy about adopting the latter, considering the large scatter in any case.

B-V values were calculated from B1-R1 using this factor of 0.556 and an 'observed minus calculated' plot derived, which was plotted against loneos V, the attached graph 'OminusC'.

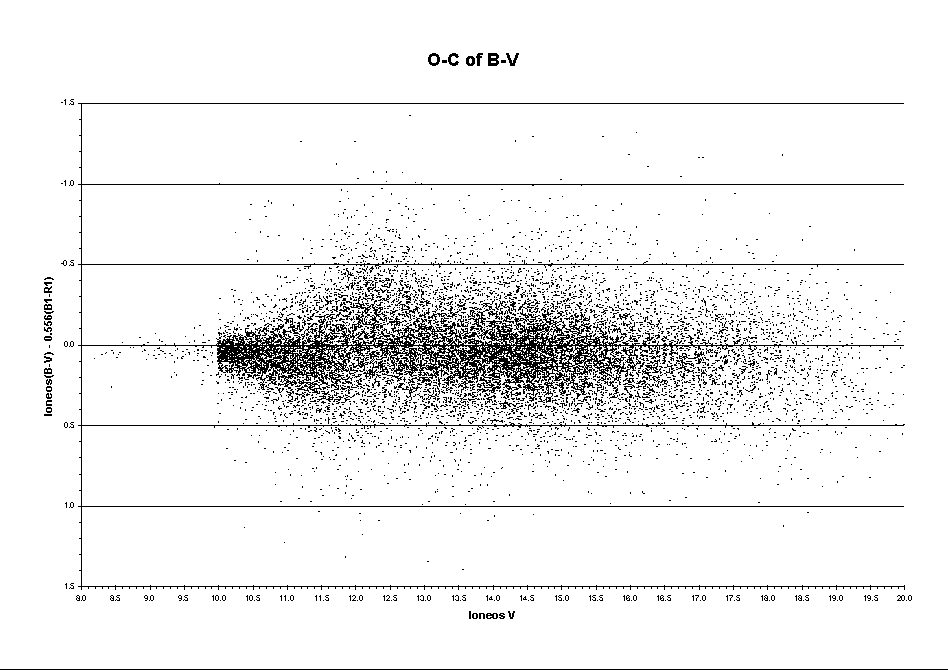
Three points deserving comment can be seen from the graph.

i) the few objects with V between 8 and 10 have very little scatter. This is simple enough to explain. These objects are probably seeded from Tycho2 and B1-R1 are in fact direct from BT and VT.

ii) the relationship between B1-R1 and B-V seems to be _remarkably_ independent of magnitude from bright to faintest, except...

iii) ...there is a strange kink in the O-C plot from around V = 11.5 to about 12.5, centred on V =12, in the sense that calculated B-V is just that bit redder than true B-V relative to other magnitudes. The kink indeed seems to show a definite structure/trend, arcing out and returning to the general trend in a symmetrical manner. Whether this represents the point where images just start to be overexposed, with a swap from one type of calibration method to another, or the practical lower limit of Tycho2 (there are known problems with Tycho2 at the faint end, which is about here), or something else altogether, I do not know.

The mean of these approximately 22,000 O-C values is 0.05 and the standard deviation is 0.24.

0.05 isn't too bad an offset, so in general the relationship

B-V = 0.556(B1-R1) +/- 0.24

allows USNO B1.0 B1-R1 'colour' to be used to derive an approximate value for B-V.

Blue, 'early' type objects and red, 'late' objects should be easy enough to distinguish, though 'yellow' objects will still be problematic because the errors are large enough for them to be actually blue or red, and this over and above the fact that yellow objects can in any case be blue objects disguised by reddenning.

In any case, despite some small number of ridiculous results which are readily discounted (large negative or positive B1-R1 values), USNO B1.0 B1-R1 seems at least a usable set of data in first instance cases where an idea of colour would be useful.

It should not be considered rigorous though. Yet it is preferable to not infrequent instances I have seen of blind usage of USNO Ax and/or GSC2.2 blue and red colours which should have been instantly obvious as peculiar due to their large value, and on investigation turned out to be due to being multi-epoch images of a variable star rather than being due to colour.

An assessment of the blue and red magnitudes, individually, showed that USNO B1.0 B1 magnitudes were equal to Johnson B magnitudes such that B1 = B, with a better relationship (correlation coefficient about 0.85) than in the B-V case. However, this is still not a firm fit, and indeed the standard deviation on B1-B was 0.5.

A similar result can be estimated for R1 versus Cousins' R.

So, it is no great surprise that the same result occured in the standard deviation for V as calculated from B1 and R1 against Johnson V, namely 0.5.

That is:

Johnson B = USNO B1.0 B1 +/- 0.5

Johnson R = USNO B1.0 R1 +/- 0.5

V = 0.444B1 + 0.556R1 +/- 0.5

In other words, V calculated from USNO B1.0 B1 and R1 are no better than using GSC1.x magnitudes directly, the latter itself being a normally decried practice.

In summary: V magnitudes from B1 and R1 are really not suitable for any use, except possibly when there is no other alternative whatsoever.