|
The scheduler adjusts the energy U of each element depending on the
surrounding environment.
The stronger energy means that you should observe the comet at the time
much more.
Finally, if 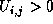 is satisfied, it concludes to observe comet
i at the time j and sets is satisfied, it concludes to observe comet
i at the time j and sets 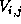 as 1. as 1.
The value of energy is limited as 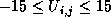 . .
At first, initialize 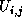 so that the better the condition is, the
larger the energy of the time comes.
Here so that the better the condition is, the
larger the energy of the time comes.
Here 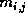 means the corrected magnitude of comet i at time j, means the corrected magnitude of comet i at time j,
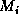 means the brightest corrected magnitude of comet i.
First, define the square of comet i, means the brightest corrected magnitude of comet i.
First, define the square of comet i, 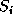 , as follows: , as follows:

If the condition of the comet doesn't change all through a night, it has
a smallest square 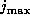 .
Here, .
Here, 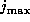 is the number of times.
In that case, the system gives least weight to each time j to observe
comet i at the time, because the comet can be observed anytime.
On the other hand, if the square is large, the system gives much weight
to good condition times because the comet can be observed at only those
times.
Considering those points, the initial energy is defined as follows: is the number of times.
In that case, the system gives least weight to each time j to observe
comet i at the time, because the comet can be observed anytime.
On the other hand, if the square is large, the system gives much weight
to good condition times because the comet can be observed at only those
times.
Considering those points, the initial energy is defined as follows:
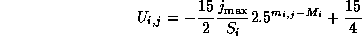
The definition of the difference of 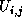 at a step, at a step, 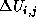 , is as follows.
Here , is as follows.
Here 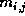 means the corrected magnitude of comet i at the time
j and means the corrected magnitude of comet i at the time
j and 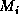 is the brightest value among the corrected magnitude of
comet i.
At first, it sets is the brightest value among the corrected magnitude of
comet i.
At first, it sets 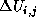 as 0, then submits the following
rules. as 0, then submits the following
rules.
- Increase
- No time to observe the comet.
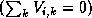
If no other comets should be observed at time j, increases the energy.
The brighter the corrected magnitude is, which means the condition is
better, the more the energy increases.
When a comet has already occupy the time, it does not increase the
energy.
But if you prefer to brighter comets and the corrected magnitude of
comet i is brighter, the system increases the energy.
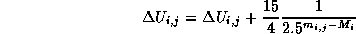
- Decrease
- More than 2 comets to observe at the time.
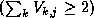
The more observable time blocks the comet has, the more the energy decreases.
If you prefer to brighter comets and one of the comets which should be
observed at the same time is brighter than comet i, decrease 2 moreover.
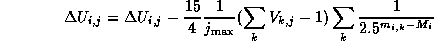
- More than 2 time blocks to observe the comet.
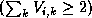
The fainter the corrected magnitude is, which means the condition is
worse, the more the energy decreases.
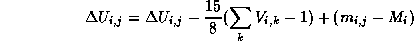
- Random
To avoid falling into a local minimum, the system uses random.
In 10% case, it adds 1 to 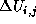 , in other 10% case, it
subtracts 1 from , in other 10% case, it
subtracts 1 from 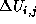 . .
When 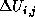 is calculated, is calculated,

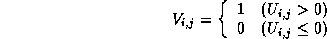
and goes to next step.
The energy adjustment of each element is not a parallel process.
The scheduler changes each 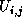 one by one from one by one from 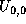 to to
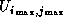 .
Therefore, when .
Therefore, when 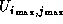 is adjusted, all the other
elements have been adjusted already and is adjusted, all the other
elements have been adjusted already and 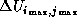 is calculated with the new
is calculated with the new 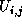 and and 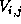 . .
|
![]()
![]()
![]()
![]()